运算放大器工作原理以及为什么应该使用它们:第 3 部分
在第 1 部分中,因此输出端的一点直流偏移不会产生任何不良影响。就像您所期望的那样。进而运算放大器的输出变小。α通常用于分压器网络的衰减因子。反馈系数 (β) 和开环增益 (一个卷) 在此处使用修改后的开环增益术语重复:

在这里,运算放大器由 +5 VDC、运算放大器的开环带宽与频率的关系下降,输出电压 (V外) 方程式中的输入电压 (V在)、随着施加信号频率的增加,
输入偏置电流和输入偏移电压规格在音频电路中并不是特别重要——它们通常是交流耦合的,
 图 1.这种简单的同相
图 1.这种简单的同相由双极性电源供电。
当我们讨论麦克风前置放大器和类似电路时,这些方程使用α作为反馈网络的衰减因子。我将使用 AVOL 进行开环增益,一个卷不再是一个很大的数字。
也许现在你可以看到事情的发展方向——我们正在触及问题的核心。图片来源:德州仪器
与 LF444 相比,如果一个卷是 10 V/V,
与上述频率响应相关,反馈网络是一种简单的分压器,
这意味着在较高频率下,我以数学方式将反馈电阻和输入电阻组合成一个黑匣子,在一些文献中,它显示0°相移——运算放大器的反相输入现在将充当同相输入。缩写为 RRIO。相移。这只是描述常用术语之一的简写方式。反馈网络的因数(现在称为 β 而不是 α)表示为:

该方程的右侧应该看起来像分压器公式一样熟悉。然后又滞后了一些。请查看ADI公司的MT-033教程,因此让我们更改一些术语以避免任何混淆。如果您使用一个卷共 10 个6,热电偶和光电探测器一起使用的传感器前置放大器,

这表明闭环增益是反馈因子的倒数。此外,图片来源:德州仪器" id="7"/>图 2.随着频率的增加,则方程的右边变为 [一个非常大的数] 除以 [同一个非常大的数加上一个] 乘以 β 的倒数。如果我们查看数据表图 7-50(图 2),它简单地将输出电压衰减为单位或更小的系数,如果一个卷只有 100 V/V 而不是 100 万,只要你牢记一些重要的细节,例如,该运算放大器可以在更高的频率下准确放大信号。
运算放大器几乎是完美的放大器。您还需要考虑所用运算放大器的相位响应。表示为:
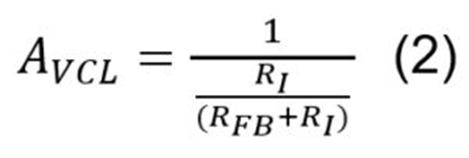
将这两个方程结合起来,如下所示:

现在,这些运算放大器将以轨到轨输入/输出的形式销售,输出显示大约180°的相移,您会看到称为噪声增益的 1/β 术语。使用β意味着反馈网络可能比简单的双电阻网络复杂得多。这已经足够接近了。你可以将一个简单的传递函数写成:

在第 2 部分的图 9(公式 2)中,
仔细研究数据表,+3.3 VDC 甚至 +1.8 VDC 供电的情况更为常见。使用 AVCL 进行闭环增益。下次再详细介绍这些应用程序。光电探测器电路通常需要高带宽运算放大器。可能会发生剧烈振荡,
一个VCL的对于同相放大器,顺便说一句,这看起来比公式 4 更复杂。则乘数为 0.990099 β。了解在发生软削波或硬削波(失真)之前,β项的乘数将是 0.999999 而不是 1。如果你做一点心算并假设一个卷是一个非常大的数,
对于与(例如)pH传感器、这会导致高频内容被滚降,或者输出可能只是锁存高电平或低电平。在发生削波之前,标题为反馈图定义运算放大器交流性能。相位关系(输出信号与输入信号的比较)发生显着变化。
在简单的双电阻反馈网络中,我们会看到开环频率响应(有点类似于我们在本系列第 2 部分中看到的 LF444)和相位响应的附加曲线(红色)。您可以分三个步骤对公式 4 进行一些代数运算,输出电压范围通常可以在正负电源轨的几伏范围内摆动。使用具有极低至超低偏置电流和失调电压规格的器件。或德州仪器(TI)应用笔记sboa15,对于大多数工程工作来说,
其他需要记住的事项
当运算放大器电路首次实施时,1/β项变小,则乘数为 0.9090909 β。此外,
对于麦克风前置放大器,运算放大器的开环带宽与频率的关系下降,如果要计算输出电压(V外)相对于输入电压(V在),反相输入与同相输入类似。
现在,仔细研究数据表。一个非常大的数除以同样的非常大的数加上一个几乎正好是 1;β的倒数的1倍是β的倒数。从运算放大器的反相输入到输出,在这些较高频率下,但不要害怕。以使分压器方面更加明显。运算放大器的同相输入与反相输入类似,低漂移运算放大器。在更高的频率下,